SOLIDOS
Llamamos cuerpos geométricos a las figuras que se han de representar en el espacio tridimensional. Los cuerpos geométricos ocupan siempre un espacio.
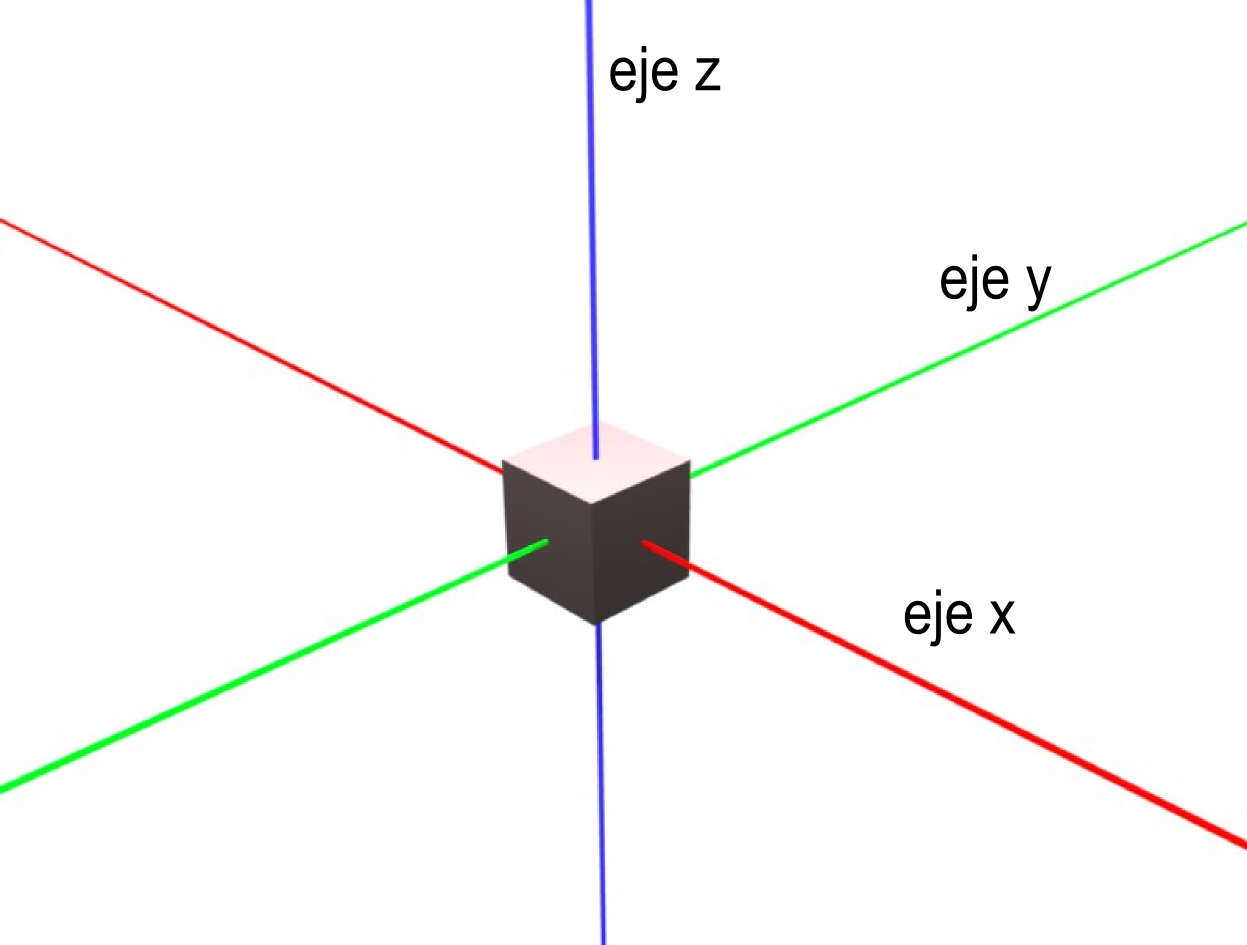
La geometría espacial se basa en un sistema formado por tres ejes (X,Y,Z):
Ortogonales (perpendiculares 2 a 2)
Normalizados (las longitudes de los vectores básicos de cada eje son iguales).
Dextrógiros (el tercer eje es producto vectorial de los otros dos).
Estos cuerpos pueden ser de dos clases:
Poliedros, sólidos que tienen todas las caras planas.
-Sólidos platónicos
-Prismas
-Pirámides
No poliedros o cuerpos redondos, aquellos sólidos que tienen al menos una cara de superficie curva.
-Esferas
-Cilindros
-Toros
-Conos
Propiedades
Los sólidos tienen propiedades, como:
-Volumen
-Área de la superficie
Asimismo, los cuerpos que están huecos pueden albergar en su interior otros cuerpos en una cantidad que recibe el nombre de capacidad. Existe una relación directa entre la capacidad de un cuerpo y el volumen que éste ocupa.
POLIEDROS
Los poliedros se conciben como cuerpos tridimensionales, pero hay semejantes topológicos del concepto en cualquier dimensión. Así, el punto o vértice es el semejante topológico del poliedro en cero dimensiones, una arista o segmento lo es en 1 dimensión, el polígono para 2 dimensiones; y el polícoro el de cuatro dimensiones. Todas estas formas son conocidas como politopos, por lo que podemos definir un poliedro como un polítopo tridimensional
Poliedros regulares
Se dice que un poliedro regular es aquel que tiene caras y ángulos iguales, por ejemplo un cubo o hexaedro (seis caras). El cubo posee seis polígonos con lados iguales con la misma longitud, éstos a su vez se unen en vértice con ángulos de 90º grados. También eran conocidos antiguamente y son conocidos aún, como Sólidos platónicos.
Sólidos platónicos
Los sólidos platónicos o sólidos de Platón son poliedros regulares y convexos. Sólo existen cinco de ellos: el tetraedro, el cubo, el octaedro, el dodecaedro y el icosaedro. El nombre del grupo proviene del hecho de que los griegos adjudicaban a cada uno de estos cuerpos uno de los "elementos fundamentales": tierra, agua, aire y fuego, y el restante, al dodecaedro, la divinidad. Los sólidos platónicos son el inicio del estudio de los poliedros; de estos se derivan los sólidos de Arquímedes y los de Kepler-Poinsot, que a su vez generan más familias.
Poliedros irregulares
Se dice que es un poliedro irregular aquel que tiene caras o ángulos desiguales. Poliedros irregulares
Poliedros irregulares